Convolutional Gaussian Processes#
Mark van der Wilk (July 2019)
Here we show a simple example of the rectangles experiment, where we compare a normal squared exponential GP, and a convolutional GP. This is similar to the experiment in [1].
[1] Van der Wilk, Rasmussen, Hensman (2017). Convolutional Gaussian Processes. Advances in Neural Information Processing Systems 30.
Generate dataset#
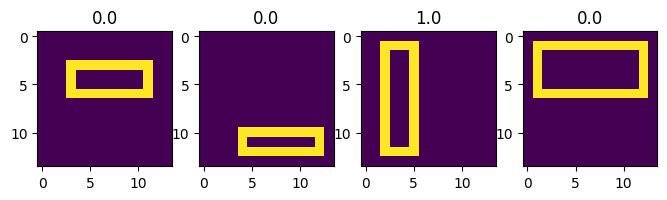
Generate a simple dataset of rectangles. We want to classify whether they are tall or wide. NOTE: Here we take care to make sure that the rectangles don’t touch the edge, which is different to the original paper. We do this to avoid needing to use patch weights, which are needed to correctly account for edge effects.
[1]:
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
import gpflow
from gpflow import set_trainable
from gpflow.ci_utils import is_continuous_integration
gpflow.config.set_default_float(np.float64)
gpflow.config.set_default_jitter(1e-4)
gpflow.config.set_default_summary_fmt("notebook")
# for reproducibility of this notebook:
np.random.seed(123)
tf.random.set_seed(42)
MAXITER = 2 if is_continuous_integration() else 100
NUM_TRAIN_DATA = (
5 if is_continuous_integration() else 100
) # This is less than in the original rectangles dataset
NUM_TEST_DATA = 7 if is_continuous_integration() else 300
H = W = 14 # width and height. In the original paper this is 28
IMAGE_SHAPE = [H, W]
2023-08-09 12:25:37.055770: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT
[2]:
def affine_scalar_bijector(shift=None, scale=None):
scale_bijector = (
tfp.bijectors.Scale(scale) if scale else tfp.bijectors.Identity()
)
shift_bijector = (
tfp.bijectors.Shift(shift) if shift else tfp.bijectors.Identity()
)
return shift_bijector(scale_bijector)
def make_rectangle(arr, x0, y0, x1, y1):
arr[y0:y1, x0] = 1
arr[y0:y1, x1] = 1
arr[y0, x0:x1] = 1
arr[y1, x0 : x1 + 1] = 1
def make_random_rectangle(arr):
x0 = np.random.randint(1, arr.shape[1] - 3)
y0 = np.random.randint(1, arr.shape[0] - 3)
x1 = np.random.randint(x0 + 2, arr.shape[1] - 1)
y1 = np.random.randint(y0 + 2, arr.shape[0] - 1)
make_rectangle(arr, x0, y0, x1, y1)
return x0, y0, x1, y1
def make_rectangles_dataset(num, w, h):
d, Y = np.zeros((num, h, w)), np.zeros((num, 1))
for i, img in enumerate(d):
for j in range(1000): # Finite number of tries
x0, y0, x1, y1 = make_random_rectangle(img)
rw, rh = y1 - y0, x1 - x0
if rw == rh:
img[:, :] = 0
continue
Y[i, 0] = rw > rh
break
return (
d.reshape(num, w * h).astype(gpflow.config.default_float()),
Y.astype(gpflow.config.default_float()),
)
[3]:
X, Y = data = make_rectangles_dataset(NUM_TRAIN_DATA, *IMAGE_SHAPE)
Xt, Yt = test_data = make_rectangles_dataset(NUM_TEST_DATA, *IMAGE_SHAPE)
[4]:
plt.figure(figsize=(8, 3))
for i in range(4):
plt.subplot(1, 4, i + 1)
plt.imshow(X[i, :].reshape(*IMAGE_SHAPE))
plt.title(Y[i, 0])
Squared Exponential kernel#
[5]:
rbf_m = gpflow.models.SVGP(
gpflow.kernels.SquaredExponential(),
gpflow.likelihoods.Bernoulli(),
gpflow.inducing_variables.InducingPoints(X.copy()),
)
[6]:
rbf_training_loss_closure = rbf_m.training_loss_closure(data, compile=True)
rbf_elbo = lambda: -rbf_training_loss_closure().numpy()
print("RBF elbo before training: %.4e" % rbf_elbo())
RBF elbo before training: -9.9408e+01
[7]:
set_trainable(rbf_m.inducing_variable, False)
start_time = time.time()
res = gpflow.optimizers.Scipy().minimize(
rbf_training_loss_closure,
variables=rbf_m.trainable_variables,
method="l-bfgs-b",
options={"disp": True, "maxiter": MAXITER},
)
print(f"{res.nfev / (time.time() - start_time):.3f} iter/s")
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 5152 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 9.94077D+01 |proj g|= 1.77693D+01
At iterate 1 f= 8.27056D+01 |proj g|= 1.08235D+01
At iterate 2 f= 7.10286D+01 |proj g|= 2.52642D+00
At iterate 3 f= 6.96128D+01 |proj g|= 9.52086D-01
At iterate 4 f= 6.91601D+01 |proj g|= 2.98596D-01
At iterate 5 f= 6.90683D+01 |proj g|= 4.57667D-01
At iterate 6 f= 6.87999D+01 |proj g|= 8.48569D-01
At iterate 7 f= 6.87526D+01 |proj g|= 1.00002D+00
At iterate 8 f= 6.85857D+01 |proj g|= 1.28576D+00
At iterate 9 f= 6.81708D+01 |proj g|= 2.04265D+00
At iterate 10 f= 6.58595D+01 |proj g|= 1.34225D+00
At iterate 11 f= 6.47617D+01 |proj g|= 9.21923D-01
At iterate 12 f= 6.37115D+01 |proj g|= 7.98398D-01
At iterate 13 f= 6.31593D+01 |proj g|= 3.96800D-01
At iterate 14 f= 6.23801D+01 |proj g|= 1.27642D+00
At iterate 15 f= 6.17198D+01 |proj g|= 7.71734D-01
At iterate 16 f= 6.13083D+01 |proj g|= 6.72739D-01
At iterate 17 f= 6.09537D+01 |proj g|= 4.45487D-01
At iterate 18 f= 6.07507D+01 |proj g|= 5.04335D-01
At iterate 19 f= 6.06242D+01 |proj g|= 1.80232D-01
At iterate 20 f= 6.04829D+01 |proj g|= 1.79481D-01
At iterate 21 f= 6.04182D+01 |proj g|= 1.66211D-01
At iterate 22 f= 6.04028D+01 |proj g|= 1.52839D-01
At iterate 23 f= 6.03795D+01 |proj g|= 4.28437D-02
At iterate 24 f= 6.03764D+01 |proj g|= 4.87340D-02
At iterate 25 f= 6.03741D+01 |proj g|= 3.66168D-02
At iterate 26 f= 6.03735D+01 |proj g|= 1.01438D-01
At iterate 27 f= 6.03723D+01 |proj g|= 3.97105D-02
At iterate 28 f= 6.03721D+01 |proj g|= 1.89009D-02
At iterate 29 f= 6.03719D+01 |proj g|= 1.17457D-02
At iterate 30 f= 6.03716D+01 |proj g|= 1.04475D-02
This problem is unconstrained.
At iterate 31 f= 6.03716D+01 |proj g|= 1.80645D-02
At iterate 32 f= 6.03714D+01 |proj g|= 2.73618D-03
At iterate 33 f= 6.03714D+01 |proj g|= 2.05487D-03
At iterate 34 f= 6.03714D+01 |proj g|= 2.28429D-03
At iterate 35 f= 6.03714D+01 |proj g|= 2.56206D-03
At iterate 36 f= 6.03714D+01 |proj g|= 8.80378D-04
At iterate 37 f= 6.03714D+01 |proj g|= 3.83350D-04
At iterate 38 f= 6.03714D+01 |proj g|= 3.14405D-04
At iterate 39 f= 6.03714D+01 |proj g|= 2.42994D-04
At iterate 40 f= 6.03714D+01 |proj g|= 5.85343D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
5152 40 48 1 0 0 5.853D-04 6.037D+01
F = 60.371382131218326
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
39.054 iter/s
[8]:
train_acc = np.mean((rbf_m.predict_y(X)[0] > 0.5).numpy().astype("float") == Y)
test_acc = np.mean((rbf_m.predict_y(Xt)[0] > 0.5).numpy().astype("float") == Yt)
print(f"Train acc: {train_acc * 100}%\nTest acc : {test_acc*100}%")
print("RBF elbo after training: %.4e" % rbf_elbo())
Train acc: 100.0%
Test acc : 68.33333333333333%
RBF elbo after training: -6.0371e+01
Convolutional kernel#
[9]:
f64 = lambda x: np.array(x, dtype=np.float64)
positive_with_min = lambda: affine_scalar_bijector(shift=f64(1e-4))(
tfp.bijectors.Softplus()
)
constrained = lambda: affine_scalar_bijector(shift=f64(1e-4), scale=f64(100.0))(
tfp.bijectors.Sigmoid()
)
max_abs_1 = lambda: affine_scalar_bijector(shift=f64(-2.0), scale=f64(4.0))(
tfp.bijectors.Sigmoid()
)
patch_shape = [3, 3]
conv_k = gpflow.kernels.Convolutional(
gpflow.kernels.SquaredExponential(), IMAGE_SHAPE, patch_shape
)
conv_k.base_kernel.lengthscales = gpflow.Parameter(
1.0, transform=positive_with_min()
)
# Weight scale and variance are non-identifiable. We also need to prevent variance from shooting off crazily.
conv_k.base_kernel.variance = gpflow.Parameter(1.0, transform=constrained())
conv_k.weights = gpflow.Parameter(conv_k.weights.numpy(), transform=max_abs_1())
conv_f = gpflow.inducing_variables.InducingPatches(
np.unique(conv_k.get_patches(X).numpy().reshape(-1, 9), axis=0)
)
[10]:
conv_m = gpflow.models.SVGP(conv_k, gpflow.likelihoods.Bernoulli(), conv_f)
[11]:
set_trainable(conv_m.inducing_variable, False)
set_trainable(conv_m.kernel.base_kernel.variance, False)
set_trainable(conv_m.kernel.weights, False)
[12]:
conv_training_loss_closure = conv_m.training_loss_closure(data, compile=True)
conv_elbo = lambda: -conv_training_loss_closure().numpy()
print("conv elbo before training: %.4e" % conv_elbo())
conv elbo before training: -8.7271e+01
[13]:
start_time = time.time()
res = gpflow.optimizers.Scipy().minimize(
conv_training_loss_closure,
variables=conv_m.trainable_variables,
method="l-bfgs-b",
options={"disp": True, "maxiter": MAXITER / 10},
)
print(f"{res.nfev / (time.time() - start_time):.3f} iter/s")
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1081 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 8.72706D+01 |proj g|= 3.34786D+01
At iterate 1 f= 7.06198D+01 |proj g|= 1.23134D+01
This problem is unconstrained.
At iterate 2 f= 7.03607D+01 |proj g|= 6.56137D+00
At iterate 3 f= 6.98680D+01 |proj g|= 2.96447D+00
At iterate 4 f= 6.93739D+01 |proj g|= 2.88465D+00
At iterate 5 f= 6.88717D+01 |proj g|= 5.27202D+00
At iterate 6 f= 6.60134D+01 |proj g|= 1.11323D+01
At iterate 7 f= 6.51602D+01 |proj g|= 3.43289D+00
At iterate 8 f= 6.49795D+01 |proj g|= 9.75563D-01
At iterate 9 f= 6.48808D+01 |proj g|= 9.60694D-01
At iterate 10 f= 6.48453D+01 |proj g|= 1.39257D+00
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1081 10 11 1 0 0 1.393D+00 6.485D+01
F = 64.845328136876162
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT
5.258 iter/s
[14]:
set_trainable(conv_m.kernel.base_kernel.variance, True)
res = gpflow.optimizers.Scipy().minimize(
conv_training_loss_closure,
variables=conv_m.trainable_variables,
method="l-bfgs-b",
options={"disp": True, "maxiter": MAXITER},
)
train_acc = np.mean((conv_m.predict_y(X)[0] > 0.5).numpy().astype("float") == Y)
test_acc = np.mean(
(conv_m.predict_y(Xt)[0] > 0.5).numpy().astype("float") == Yt
)
print(f"Train acc: {train_acc * 100}%\nTest acc : {test_acc*100}%")
print("conv elbo after training: %.4e" % conv_elbo())
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1082 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 6.48453D+01 |proj g|= 3.53996D+00
At iterate 1 f= 6.24919D+01 |proj g|= 7.35357D+00
This problem is unconstrained.
At iterate 2 f= 6.23531D+01 |proj g|= 7.58264D+00
At iterate 3 f= 6.04166D+01 |proj g|= 1.58157D+01
At iterate 4 f= 5.88887D+01 |proj g|= 2.48005D+01
At iterate 5 f= 5.63927D+01 |proj g|= 4.28536D+01
At iterate 6 f= 5.02144D+01 |proj g|= 1.04313D+02
At iterate 7 f= 4.44685D+01 |proj g|= 8.74280D+01
At iterate 8 f= 3.92359D+01 |proj g|= 3.11481D+01
At iterate 9 f= 3.74686D+01 |proj g|= 3.06073D+01
At iterate 10 f= 3.68864D+01 |proj g|= 4.40037D+01
At iterate 11 f= 3.60668D+01 |proj g|= 7.87412D+00
At iterate 12 f= 3.58935D+01 |proj g|= 1.41535D+01
At iterate 13 f= 3.45651D+01 |proj g|= 7.04865D+01
At iterate 14 f= 3.13752D+01 |proj g|= 4.56939D+01
At iterate 15 f= 3.02012D+01 |proj g|= 2.86627D+01
At iterate 16 f= 2.96655D+01 |proj g|= 1.60272D+01
At iterate 17 f= 2.94558D+01 |proj g|= 8.24031D+00
At iterate 18 f= 2.93105D+01 |proj g|= 2.25261D+00
At iterate 19 f= 2.90992D+01 |proj g|= 5.73397D+00
At iterate 20 f= 2.87163D+01 |proj g|= 1.55953D+01
At iterate 21 f= 2.81823D+01 |proj g|= 2.54265D+01
At iterate 22 f= 2.80343D+01 |proj g|= 2.19902D+01
At iterate 23 f= 2.79432D+01 |proj g|= 1.41609D+01
At iterate 24 f= 2.78263D+01 |proj g|= 2.44911D+00
At iterate 25 f= 2.78000D+01 |proj g|= 1.18706D+00
At iterate 26 f= 2.77623D+01 |proj g|= 3.27247D+00
At iterate 27 f= 2.76356D+01 |proj g|= 5.23204D+00
At iterate 28 f= 2.74130D+01 |proj g|= 6.84226D+00
At iterate 29 f= 2.72099D+01 |proj g|= 2.39793D+00
At iterate 30 f= 2.71505D+01 |proj g|= 8.87291D-01
At iterate 31 f= 2.71225D+01 |proj g|= 1.25368D+00
At iterate 32 f= 2.70691D+01 |proj g|= 3.44551D+00
At iterate 33 f= 2.70246D+01 |proj g|= 3.99899D+00
At iterate 34 f= 2.70165D+01 |proj g|= 1.66840D+00
At iterate 35 f= 2.69736D+01 |proj g|= 1.96735D-01
At iterate 36 f= 2.69568D+01 |proj g|= 4.38151D+00
At iterate 37 f= 2.69408D+01 |proj g|= 1.61116D+00
At iterate 38 f= 2.69308D+01 |proj g|= 1.04302D+00
At iterate 39 f= 2.68977D+01 |proj g|= 1.50422D+00
At iterate 40 f= 2.68704D+01 |proj g|= 2.03393D+00
At iterate 41 f= 2.68478D+01 |proj g|= 7.74728D-01
At iterate 42 f= 2.68370D+01 |proj g|= 6.68973D-01
At iterate 43 f= 2.68312D+01 |proj g|= 1.17495D+00
At iterate 44 f= 2.68205D+01 |proj g|= 1.40366D+00
At iterate 45 f= 2.68164D+01 |proj g|= 2.93859D+00
At iterate 46 f= 2.68066D+01 |proj g|= 1.14149D+00
At iterate 47 f= 2.68038D+01 |proj g|= 2.29234D-01
At iterate 48 f= 2.68031D+01 |proj g|= 6.60556D-02
At iterate 49 f= 2.68025D+01 |proj g|= 6.92338D-01
At iterate 50 f= 2.68010D+01 |proj g|= 7.83827D-01
At iterate 51 f= 2.67992D+01 |proj g|= 2.75352D+00
At iterate 52 f= 2.67965D+01 |proj g|= 1.09880D+00
At iterate 53 f= 2.67954D+01 |proj g|= 1.38053D-01
At iterate 54 f= 2.67951D+01 |proj g|= 1.82728D-01
At iterate 55 f= 2.67943D+01 |proj g|= 2.35894D-01
At iterate 56 f= 2.67915D+01 |proj g|= 1.36174D+00
At iterate 57 f= 2.67888D+01 |proj g|= 1.44453D+00
At iterate 58 f= 2.67867D+01 |proj g|= 6.69400D-01
At iterate 59 f= 2.67852D+01 |proj g|= 2.49436D-01
At iterate 60 f= 2.67849D+01 |proj g|= 1.30110D-01
At iterate 61 f= 2.67838D+01 |proj g|= 3.45478D-01
At iterate 62 f= 2.67818D+01 |proj g|= 7.66751D-01
At iterate 63 f= 2.67784D+01 |proj g|= 9.01109D-01
At iterate 64 f= 2.67780D+01 |proj g|= 1.20388D+00
At iterate 65 f= 2.67748D+01 |proj g|= 8.05237D-01
At iterate 66 f= 2.67725D+01 |proj g|= 9.53573D-02
At iterate 67 f= 2.67716D+01 |proj g|= 2.91392D-01
At iterate 68 f= 2.67709D+01 |proj g|= 2.11336D-01
At iterate 69 f= 2.67707D+01 |proj g|= 7.81715D-01
At iterate 70 f= 2.67699D+01 |proj g|= 4.71523D-01
At iterate 71 f= 2.67687D+01 |proj g|= 7.84486D-02
At iterate 72 f= 2.67676D+01 |proj g|= 3.15235D-01
At iterate 73 f= 2.67667D+01 |proj g|= 4.34509D-01
At iterate 74 f= 2.67662D+01 |proj g|= 8.67849D-01
At iterate 75 f= 2.67653D+01 |proj g|= 1.22312D+00
At iterate 76 f= 2.67642D+01 |proj g|= 5.35684D-01
At iterate 77 f= 2.67634D+01 |proj g|= 5.13194D-02
At iterate 78 f= 2.67632D+01 |proj g|= 1.30113D-01
At iterate 79 f= 2.67626D+01 |proj g|= 1.95710D-01
At iterate 80 f= 2.67625D+01 |proj g|= 5.88159D-01
At iterate 81 f= 2.67616D+01 |proj g|= 3.65936D-01
At iterate 82 f= 2.67614D+01 |proj g|= 2.95283D-01
At iterate 83 f= 2.67611D+01 |proj g|= 1.94345D-01
At iterate 84 f= 2.67606D+01 |proj g|= 1.65529D-01
At iterate 85 f= 2.67587D+01 |proj g|= 1.14022D-01
At iterate 86 f= 2.67585D+01 |proj g|= 4.94482D-01
At iterate 87 f= 2.67577D+01 |proj g|= 3.20143D-01
At iterate 88 f= 2.67576D+01 |proj g|= 8.06103D-01
At iterate 89 f= 2.67569D+01 |proj g|= 2.29646D-01
At iterate 90 f= 2.67567D+01 |proj g|= 8.60409D-02
At iterate 91 f= 2.67563D+01 |proj g|= 2.82486D-01
At iterate 92 f= 2.67559D+01 |proj g|= 2.57009D-01
At iterate 93 f= 2.67557D+01 |proj g|= 6.98616D-01
At iterate 94 f= 2.67553D+01 |proj g|= 3.90014D-01
At iterate 95 f= 2.67549D+01 |proj g|= 1.35560D-01
At iterate 96 f= 2.67545D+01 |proj g|= 1.33563D-01
At iterate 97 f= 2.67542D+01 |proj g|= 2.03929D-01
At iterate 98 f= 2.67540D+01 |proj g|= 4.02593D-01
At iterate 99 f= 2.67536D+01 |proj g|= 3.68131D-01
At iterate 100 f= 2.67533D+01 |proj g|= 3.69556D-01
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1082 100 114 1 0 0 3.696D-01 2.675D+01
F = 26.753331958808452
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT
Train acc: 100.0%
Test acc : 99.0%
conv elbo after training: -2.6753e+01
[15]:
res = gpflow.optimizers.Scipy().minimize(
conv_training_loss_closure,
variables=conv_m.trainable_variables,
method="l-bfgs-b",
options={"disp": True, "maxiter": MAXITER},
)
train_acc = np.mean((conv_m.predict_y(X)[0] > 0.5).numpy().astype("float") == Y)
test_acc = np.mean(
(conv_m.predict_y(Xt)[0] > 0.5).numpy().astype("float") == Yt
)
print(f"Train acc: {train_acc * 100}%\nTest acc : {test_acc*100}%")
print("conv elbo after training: %.4e" % conv_elbo())
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1082 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.67533D+01 |proj g|= 3.69556D-01
At iterate 1 f= 2.67533D+01 |proj g|= 2.06365D-01
At iterate 2 f= 2.67533D+01 |proj g|= 3.86139D-02
At iterate 3 f= 2.67532D+01 |proj g|= 7.55833D-02
At iterate 4 f= 2.67531D+01 |proj g|= 3.20632D-01
At iterate 5 f= 2.67530D+01 |proj g|= 5.62645D-01
At iterate 6 f= 2.67527D+01 |proj g|= 6.66727D-01
At iterate 7 f= 2.67524D+01 |proj g|= 4.89510D-01
At iterate 8 f= 2.67524D+01 |proj g|= 5.42522D-01
At iterate 9 f= 2.67522D+01 |proj g|= 1.23353D-01
At iterate 10 f= 2.67522D+01 |proj g|= 1.71282D-01
At iterate 11 f= 2.67521D+01 |proj g|= 3.07164D-01
At iterate 12 f= 2.67519D+01 |proj g|= 3.64874D-01
At iterate 13 f= 2.67517D+01 |proj g|= 2.46018D-01
At iterate 14 f= 2.67515D+01 |proj g|= 7.57820D-02
At iterate 15 f= 2.67514D+01 |proj g|= 1.00336D-01
At iterate 16 f= 2.67513D+01 |proj g|= 2.49494D-01
At iterate 17 f= 2.67512D+01 |proj g|= 3.87451D-01
At iterate 18 f= 2.67510D+01 |proj g|= 4.21678D-01
At iterate 19 f= 2.67507D+01 |proj g|= 1.64757D-01
At iterate 20 f= 2.67505D+01 |proj g|= 2.41873D-01
At iterate 21 f= 2.67504D+01 |proj g|= 3.41570D-01
At iterate 22 f= 2.67503D+01 |proj g|= 2.18225D-01
At iterate 23 f= 2.67502D+01 |proj g|= 7.63585D-02
At iterate 24 f= 2.67501D+01 |proj g|= 7.14117D-02
At iterate 25 f= 2.67501D+01 |proj g|= 7.27715D-02
At iterate 26 f= 2.67499D+01 |proj g|= 5.32219D-02
At iterate 27 f= 2.67499D+01 |proj g|= 2.55878D-01
At iterate 28 f= 2.67497D+01 |proj g|= 1.21886D-01
At iterate 29 f= 2.67496D+01 |proj g|= 4.57636D-02
At iterate 30 f= 2.67496D+01 |proj g|= 4.40242D-02
At iterate 31 f= 2.67496D+01 |proj g|= 1.94792D-02
At iterate 32 f= 2.67496D+01 |proj g|= 1.02854D-01
At iterate 33 f= 2.67496D+01 |proj g|= 6.42601D-02
At iterate 34 f= 2.67495D+01 |proj g|= 4.01797D-02
At iterate 35 f= 2.67495D+01 |proj g|= 9.46539D-02
At iterate 36 f= 2.67495D+01 |proj g|= 1.81388D-01
At iterate 37 f= 2.67494D+01 |proj g|= 4.67147D-02
At iterate 38 f= 2.67494D+01 |proj g|= 4.56626D-02
At iterate 39 f= 2.67494D+01 |proj g|= 4.03325D-02
At iterate 40 f= 2.67494D+01 |proj g|= 2.37251D-02
At iterate 41 f= 2.67494D+01 |proj g|= 3.60650D-02
At iterate 42 f= 2.67494D+01 |proj g|= 1.48639D-01
At iterate 43 f= 2.67494D+01 |proj g|= 1.04997D-01
At iterate 44 f= 2.67493D+01 |proj g|= 8.52702D-02
At iterate 45 f= 2.67493D+01 |proj g|= 2.24150D-01
At iterate 46 f= 2.67492D+01 |proj g|= 2.77971D-02
At iterate 47 f= 2.67492D+01 |proj g|= 7.01161D-02
At iterate 48 f= 2.67492D+01 |proj g|= 5.04371D-02
At iterate 49 f= 2.67492D+01 |proj g|= 5.91164D-02
At iterate 50 f= 2.67492D+01 |proj g|= 3.42234D-02
At iterate 51 f= 2.67492D+01 |proj g|= 1.35007D-01
At iterate 52 f= 2.67491D+01 |proj g|= 2.08262D-01
At iterate 53 f= 2.67490D+01 |proj g|= 2.03729D-01
At iterate 54 f= 2.67490D+01 |proj g|= 1.75642D-01
At iterate 55 f= 2.67490D+01 |proj g|= 8.25489D-02
At iterate 56 f= 2.67489D+01 |proj g|= 5.03603D-02
At iterate 57 f= 2.67489D+01 |proj g|= 9.15719D-02
At iterate 58 f= 2.67488D+01 |proj g|= 3.15185D-01
At iterate 59 f= 2.67488D+01 |proj g|= 2.94135D-01
At iterate 60 f= 2.67487D+01 |proj g|= 3.20700D-01
At iterate 61 f= 2.67485D+01 |proj g|= 1.75814D-01
At iterate 62 f= 2.67484D+01 |proj g|= 3.29942D-02
At iterate 63 f= 2.67483D+01 |proj g|= 1.17542D-01
At iterate 64 f= 2.67482D+01 |proj g|= 1.50787D-01
At iterate 65 f= 2.67481D+01 |proj g|= 3.88446D-01
At iterate 66 f= 2.67477D+01 |proj g|= 1.76959D-01
At iterate 67 f= 2.67475D+01 |proj g|= 4.17387D-02
At iterate 68 f= 2.67473D+01 |proj g|= 1.14275D-01
At iterate 69 f= 2.67472D+01 |proj g|= 1.79496D-01
At iterate 70 f= 2.67471D+01 |proj g|= 6.84332D-02
At iterate 71 f= 2.67470D+01 |proj g|= 5.70335D-02
At iterate 72 f= 2.67467D+01 |proj g|= 6.72707D-02
At iterate 73 f= 2.67466D+01 |proj g|= 3.05473D-01
At iterate 74 f= 2.67465D+01 |proj g|= 1.82233D-01
At iterate 75 f= 2.67463D+01 |proj g|= 6.06469D-02
At iterate 76 f= 2.67461D+01 |proj g|= 1.38709D-01
At iterate 77 f= 2.67456D+01 |proj g|= 3.56594D-01
At iterate 78 f= 2.67451D+01 |proj g|= 3.11022D-01
At iterate 79 f= 2.67450D+01 |proj g|= 5.90648D-01
At iterate 80 f= 2.67444D+01 |proj g|= 2.48865D-01
At iterate 81 f= 2.67443D+01 |proj g|= 7.33044D-02
At iterate 82 f= 2.67442D+01 |proj g|= 9.89315D-02
At iterate 83 f= 2.67440D+01 |proj g|= 2.31826D-01
At iterate 84 f= 2.67435D+01 |proj g|= 3.62591D-01
At iterate 85 f= 2.67428D+01 |proj g|= 6.75926D-01
At iterate 86 f= 2.67423D+01 |proj g|= 4.89902D-01
At iterate 87 f= 2.67418D+01 |proj g|= 2.96004D-01
At iterate 88 f= 2.67414D+01 |proj g|= 1.27813D-01
At iterate 89 f= 2.67407D+01 |proj g|= 1.62477D-01
At iterate 90 f= 2.67399D+01 |proj g|= 3.14672D-01
At iterate 91 f= 2.67392D+01 |proj g|= 5.17359D-01
At iterate 92 f= 2.67390D+01 |proj g|= 1.54427D-01
At iterate 93 f= 2.67388D+01 |proj g|= 9.84208D-02
At iterate 94 f= 2.67387D+01 |proj g|= 7.62589D-02
At iterate 95 f= 2.67385D+01 |proj g|= 9.58118D-02
At iterate 96 f= 2.67383D+01 |proj g|= 1.18687D-01
At iterate 97 f= 2.67382D+01 |proj g|= 1.74468D-01
At iterate 98 f= 2.67380D+01 |proj g|= 7.18287D-02
At iterate 99 f= 2.67375D+01 |proj g|= 8.26550D-02
At iterate 100 f= 2.67363D+01 |proj g|= 1.57415D-01
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1082 100 111 1 0 0 1.574D-01 2.674D+01
F = 26.736287663325719
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT
Train acc: 100.0%
Test acc : 99.0%
conv elbo after training: -2.6736e+01
[16]:
set_trainable(conv_m.kernel.weights, True)
res = gpflow.optimizers.Scipy().minimize(
conv_training_loss_closure,
variables=conv_m.trainable_variables,
method="l-bfgs-b",
options={"disp": True, "maxiter": MAXITER},
)
train_acc = np.mean((conv_m.predict_y(X)[0] > 0.5).numpy().astype("float") == Y)
test_acc = np.mean(
(conv_m.predict_y(Xt)[0] > 0.5).numpy().astype("float") == Yt
)
print(f"Train acc: {train_acc * 100}%\nTest acc : {test_acc*100}%")
print("conv elbo after training: %.4e" % conv_elbo())
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1226 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.67363D+01 |proj g|= 3.15890D-01
This problem is unconstrained.
At iterate 1 f= 2.66593D+01 |proj g|= 1.23447D+01
At iterate 2 f= 2.59601D+01 |proj g|= 1.31911D+01
At iterate 3 f= 2.38946D+01 |proj g|= 5.04322D+01
At iterate 4 f= 2.21797D+01 |proj g|= 7.72697D+00
At iterate 5 f= 2.18210D+01 |proj g|= 5.20448D+00
At iterate 6 f= 2.15484D+01 |proj g|= 2.52929D+00
At iterate 7 f= 2.09121D+01 |proj g|= 1.21088D+00
At iterate 8 f= 1.96627D+01 |proj g|= 4.42157D+00
At iterate 9 f= 1.88499D+01 |proj g|= 3.41832D+00
At iterate 10 f= 1.82255D+01 |proj g|= 3.55848D+00
At iterate 11 f= 1.79084D+01 |proj g|= 2.36303D+00
At iterate 12 f= 1.78952D+01 |proj g|= 3.36235D+00
At iterate 13 f= 1.78289D+01 |proj g|= 1.01208D+00
At iterate 14 f= 1.78061D+01 |proj g|= 1.28140D+00
At iterate 15 f= 1.77800D+01 |proj g|= 4.28107D+00
At iterate 16 f= 1.77399D+01 |proj g|= 5.38815D-01
At iterate 17 f= 1.77171D+01 |proj g|= 1.45748D+00
At iterate 18 f= 1.77002D+01 |proj g|= 8.60301D-01
At iterate 19 f= 1.76745D+01 |proj g|= 3.24458D-01
At iterate 20 f= 1.76264D+01 |proj g|= 2.78105D-01
At iterate 21 f= 1.75997D+01 |proj g|= 1.23336D-01
At iterate 22 f= 1.75696D+01 |proj g|= 7.70236D-01
At iterate 23 f= 1.75675D+01 |proj g|= 1.71359D+00
At iterate 24 f= 1.75597D+01 |proj g|= 9.01336D-01
At iterate 25 f= 1.75532D+01 |proj g|= 4.75464D-01
At iterate 26 f= 1.75458D+01 |proj g|= 7.28402D-01
At iterate 27 f= 1.75438D+01 |proj g|= 1.03329D+00
At iterate 28 f= 1.75401D+01 |proj g|= 3.09040D-01
At iterate 29 f= 1.75372D+01 |proj g|= 2.97689D-01
At iterate 30 f= 1.75283D+01 |proj g|= 3.93077D-01
At iterate 31 f= 1.75172D+01 |proj g|= 4.99012D-01
At iterate 32 f= 1.75019D+01 |proj g|= 4.42903D-01
At iterate 33 f= 1.74767D+01 |proj g|= 8.11521D-01
At iterate 34 f= 1.74668D+01 |proj g|= 1.55860D+00
At iterate 35 f= 1.74598D+01 |proj g|= 2.89704D+00
At iterate 36 f= 1.74518D+01 |proj g|= 5.30937D-01
At iterate 37 f= 1.74498D+01 |proj g|= 2.79222D-01
At iterate 38 f= 1.74485D+01 |proj g|= 3.79688D-01
At iterate 39 f= 1.74466D+01 |proj g|= 1.39104D+00
At iterate 40 f= 1.74434D+01 |proj g|= 8.27033D-01
At iterate 41 f= 1.74411D+01 |proj g|= 8.58730D-01
At iterate 42 f= 1.74314D+01 |proj g|= 1.00359D+00
At iterate 43 f= 1.74250D+01 |proj g|= 9.18368D-01
At iterate 44 f= 1.74148D+01 |proj g|= 5.05909D-01
At iterate 45 f= 1.74124D+01 |proj g|= 7.85410D-01
At iterate 46 f= 1.74061D+01 |proj g|= 1.72040D+00
At iterate 47 f= 1.74016D+01 |proj g|= 9.82946D-01
At iterate 48 f= 1.73960D+01 |proj g|= 3.56201D-01
At iterate 49 f= 1.73897D+01 |proj g|= 4.66155D-01
At iterate 50 f= 1.73790D+01 |proj g|= 8.06765D-01
At iterate 51 f= 1.73687D+01 |proj g|= 6.68134D-01
At iterate 52 f= 1.73640D+01 |proj g|= 1.59985D+00
At iterate 53 f= 1.73575D+01 |proj g|= 3.21741D-01
At iterate 54 f= 1.73540D+01 |proj g|= 5.82679D-01
At iterate 55 f= 1.73476D+01 |proj g|= 7.50497D-01
At iterate 56 f= 1.73343D+01 |proj g|= 8.32714D-01
At iterate 57 f= 1.73297D+01 |proj g|= 1.87886D+00
At iterate 58 f= 1.73082D+01 |proj g|= 1.35077D+00
At iterate 59 f= 1.72966D+01 |proj g|= 1.61551D+00
At iterate 60 f= 1.72792D+01 |proj g|= 8.95599D-01
At iterate 61 f= 1.72629D+01 |proj g|= 4.38795D-01
At iterate 62 f= 1.72463D+01 |proj g|= 1.98290D-01
At iterate 63 f= 1.72448D+01 |proj g|= 1.30648D+00
At iterate 64 f= 1.72353D+01 |proj g|= 5.29832D-01
At iterate 65 f= 1.72286D+01 |proj g|= 1.86780D-01
At iterate 66 f= 1.72173D+01 |proj g|= 5.29611D-01
At iterate 67 f= 1.72027D+01 |proj g|= 6.74830D-01
At iterate 68 f= 1.72005D+01 |proj g|= 1.23360D+00
At iterate 69 f= 1.71839D+01 |proj g|= 7.81289D-01
At iterate 70 f= 1.71796D+01 |proj g|= 7.93730D-01
At iterate 71 f= 1.71718D+01 |proj g|= 4.78583D-01
At iterate 72 f= 1.71642D+01 |proj g|= 3.34851D-01
At iterate 73 f= 1.71543D+01 |proj g|= 1.65164D+00
At iterate 74 f= 1.71522D+01 |proj g|= 2.92592D-01
At iterate 75 f= 1.71470D+01 |proj g|= 2.37492D-01
At iterate 76 f= 1.71289D+01 |proj g|= 7.56450D-01
At iterate 77 f= 1.71213D+01 |proj g|= 4.03391D-01
At iterate 78 f= 1.71175D+01 |proj g|= 1.60273D-01
At iterate 79 f= 1.71117D+01 |proj g|= 6.91271D-01
At iterate 80 f= 1.71087D+01 |proj g|= 7.43123D-01
At iterate 81 f= 1.71059D+01 |proj g|= 3.98718D-01
At iterate 82 f= 1.71032D+01 |proj g|= 2.70994D-01
At iterate 83 f= 1.71007D+01 |proj g|= 1.22893D-01
At iterate 84 f= 1.70956D+01 |proj g|= 5.84796D-01
At iterate 85 f= 1.70912D+01 |proj g|= 4.92854D-01
At iterate 86 f= 1.70883D+01 |proj g|= 7.66597D-01
At iterate 87 f= 1.70864D+01 |proj g|= 6.27289D-01
At iterate 88 f= 1.70852D+01 |proj g|= 2.05707D-01
At iterate 89 f= 1.70840D+01 |proj g|= 6.16601D-02
At iterate 90 f= 1.70824D+01 |proj g|= 2.37873D-01
At iterate 91 f= 1.70809D+01 |proj g|= 2.89050D-01
At iterate 92 f= 1.70803D+01 |proj g|= 5.73995D-01
At iterate 93 f= 1.70786D+01 |proj g|= 1.65289D-01
At iterate 94 f= 1.70773D+01 |proj g|= 1.79195D-01
At iterate 95 f= 1.70754D+01 |proj g|= 2.50309D-01
At iterate 96 f= 1.70727D+01 |proj g|= 3.16541D-01
At iterate 97 f= 1.70713D+01 |proj g|= 7.87999D-01
At iterate 98 f= 1.70686D+01 |proj g|= 4.99336D-01
At iterate 99 f= 1.70672D+01 |proj g|= 7.34938D-02
At iterate 100 f= 1.70665D+01 |proj g|= 9.01578D-02
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1226 100 121 1 0 0 9.016D-02 1.707D+01
F = 17.066503593133774
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT
Train acc: 100.0%
Test acc : 96.66666666666667%
conv elbo after training: -1.7067e+01
[17]:
gpflow.utilities.print_summary(rbf_m)
| name | class | transform | prior | trainable | shape | dtype | value |
|---|---|---|---|---|---|---|---|
| SVGP.kernel.variance | Parameter | Softplus | True | () | float64 | 3.56655 | |
| SVGP.kernel.lengthscales | Parameter | Softplus | True | () | float64 | 2.75129 | |
| SVGP.inducing_variable.Z | Parameter | Identity | False | (100, 196) | float64 | [[0., 0., 0.... | |
| SVGP.q_mu | Parameter | Identity | True | (100, 1) | float64 | [[-5.78240e-01... | |
| SVGP.q_sqrt | Parameter | FillTriangular | True | (1, 100, 100) | float64 | [[[6.4475e-01, 0.0000e+00, 0.0000e+00... |
[18]:
gpflow.utilities.print_summary(conv_m)
| name | class | transform | prior | trainable | shape | dtype | value |
|---|---|---|---|---|---|---|---|
| SVGP.kernel.base_kernel.variance | Parameter | Sigmoid + Chain | True | () | float64 | 99.98292 | |
| SVGP.kernel.base_kernel.lengthscales | Parameter | Softplus + Chain | True | () | float64 | 0.64773 | |
| SVGP.kernel.weights | Parameter | Sigmoid + Chain | True | (144,) | float64 | [0.11865, 0.30752, 0.43216... | |
| SVGP.inducing_variable.Z | Parameter | Identity | False | (45, 9) | float64 | [[0., 0., 0.... | |
| SVGP.q_mu | Parameter | Identity | True | (45, 1) | float64 | [[0.00999... | |
| SVGP.q_sqrt | Parameter | FillTriangular | True | (1, 45, 45) | float64 | [[[7.2640e-02, 0.0000e+00, 0.0000e+00... |
Conclusion#
The convolutional kernel performs much better in this simple task. It demonstrates non-local generalization of the strong assumptions in the kernel.