Multiclass classification#

The multiclass classification problem is a regression problem from an input $x \in X$ to discrete labels $y \in Y$ , where $Y$ is a discrete set of size $C$ bigger than two (for $C = 2$ it is the more usual binary classification).

Labels are encoded in a one-hot fashion, that is if $C = 4$ and $y = 2$ , we note $\bar{y} = [0, 1, 0, 0]$ .

The generative model for this problem consists of:

$C$ latent functions $f = [f_{1}, . . ., f_{C}]$ with an independent Gaussian Process prior
a deterministic function that builds a discrete distribution $π (f) = [π_{1} (f_{1}), . . ., π_{C} (f_{C})]$ from the latents such that $\sum_{c} π_{c} (f_{c}) = 1$
a discrete likelihood $p (y | f) = D i s c r e t e (y; π (f)) = \prod_{c} π_{c} (f_{c})^{{\bar{y}}_{c}}$

A typical example of $π$ is the softmax function:

$π_{c} (f_{c}) \propto \exp (f_{c})$

Another convenient one is the robust max: $π_{c} (f) = {\begin{cases} 1 - ϵ, & if c = \arg max_{c} f_{c} \\ ϵ / (C - 1), & otherwise \end{cases}$

[1]:

import warnings

warnings.filterwarnings("ignore")  # ignore DeprecationWarnings from tensorflow

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from multiclass_classification import colors, plot_posterior_predictions

import gpflow
from gpflow.ci_utils import reduce_in_tests
from gpflow.utilities import print_summary, set_trainable

%matplotlib inline


# reproducibility:
np.random.seed(0)
tf.random.set_seed(123)

2024-02-07 11:46:10.357710: I external/local_tsl/tsl/cuda/cudart_stub.cc:31] Could not find cuda drivers on your machine, GPU will not be used.
2024-02-07 11:46:10.399451: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered
2024-02-07 11:46:10.399490: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered
2024-02-07 11:46:10.400789: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered
2024-02-07 11:46:10.407487: I external/local_tsl/tsl/cuda/cudart_stub.cc:31] Could not find cuda drivers on your machine, GPU will not be used.
2024-02-07 11:46:10.408536: I tensorflow/core/platform/cpu_feature_guard.cc:182] This TensorFlow binary is optimized to use available CPU instructions in performance-critical operations.
To enable the following instructions: AVX2 AVX512F FMA, in other operations, rebuild TensorFlow with the appropriate compiler flags.

2024-02-07 11:46:11.603828: W tensorflow/compiler/tf2tensorrt/utils/py_utils.cc:38] TF-TRT Warning: Could not find TensorRT

Sampling from the GP multiclass generative model#

Declaring model parameters and input#

[2]:

# Number of functions and number of data points
C = 3
N = 100

# Lengthscale of the SquaredExponential kernel (isotropic -- change to `[0.1] * C` for ARD)
lengthscales = 0.1

# Jitter
jitter_eye = np.eye(N) * 1e-6

# Input
X = np.random.rand(N, 1)

Sampling#

[3]:

# SquaredExponential kernel matrix
kernel_se = gpflow.kernels.SquaredExponential(lengthscales=lengthscales)
K = kernel_se(X) + jitter_eye

# Latents prior sample
f = np.random.multivariate_normal(mean=np.zeros(N), cov=K, size=(C)).T

# Hard max observation
Y = np.argmax(f, 1).flatten().astype(int)

# One-hot encoding
Y_hot = np.zeros((N, C), dtype=bool)
Y_hot[np.arange(N), Y] = 1

data = (X, Y)

Plotting#

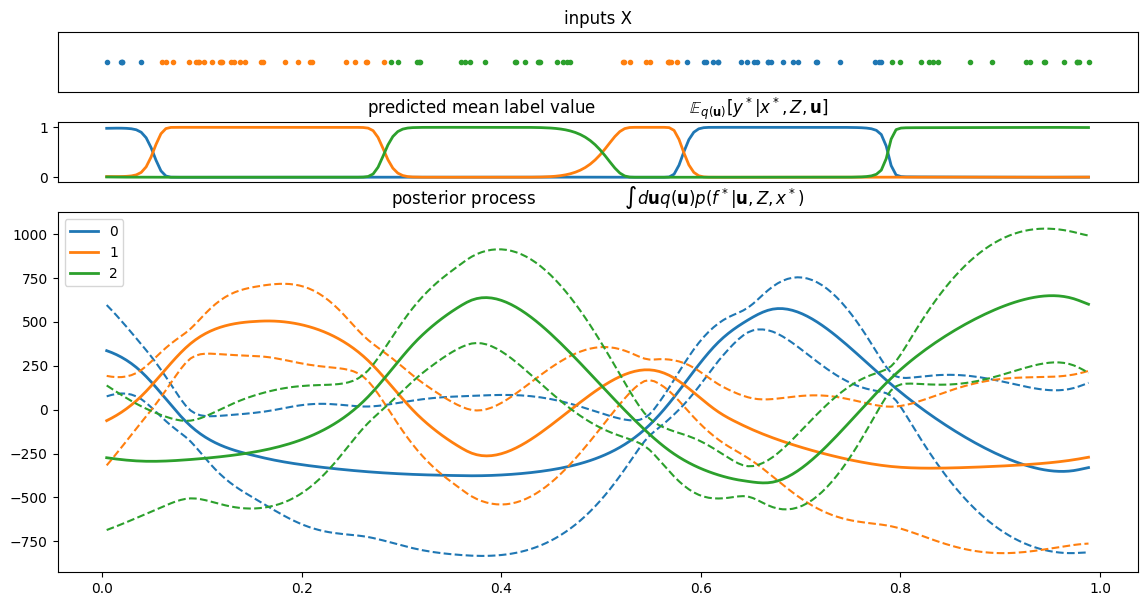
[4]:

plt.figure(figsize=(12, 6))
order = np.argsort(X.flatten())

for c in range(C):
    plt.plot(X[order], f[order, c], ".", color=colors[c], label=str(c))
    plt.plot(X[order], Y_hot[order, c], "-", color=colors[c])


plt.legend()
plt.xlabel("$X$")
plt.ylabel("Latent (dots) and one-hot labels (lines)")
plt.title("Sample from the joint $p(Y, \mathbf{f})$")
plt.grid()
plt.show()

../../_images/notebooks_advanced_multiclass_classification_9_0.png

Inference#

Inference here consists of computing the posterior distribution over the latent functions given the data $p (f | Y, X)$ .

You can use different inference methods. Here we perform variational inference. For a treatment of the multiclass classification problem using MCMC sampling, see Markov Chain Monte Carlo (MCMC).

Approximate inference: Sparse Variational Gaussian Process#

Declaring the SVGP model (see GPs for big data)#

[5]:

# sum kernel: Matern32 + White
kernel = gpflow.kernels.Matern32() + gpflow.kernels.White(variance=0.01)

# Robustmax Multiclass Likelihood
invlink = gpflow.likelihoods.RobustMax(C)  # Robustmax inverse link function
likelihood = gpflow.likelihoods.MultiClass(
    3, invlink=invlink
)  # Multiclass likelihood
Z = X[::5].copy()  # inducing inputs

m = gpflow.models.SVGP(
    kernel=kernel,
    likelihood=likelihood,
    inducing_variable=Z,
    num_latent_gps=C,
    whiten=True,
    q_diag=True,
)

# Only train the variational parameters
set_trainable(m.kernel.kernels[1].variance, False)
set_trainable(m.inducing_variable, False)
print_summary(m, fmt="notebook")

name	class	transform	prior	trainable	shape	dtype	value
SVGP.kernel.kernels[0].variance	Parameter	Softplus		True	()	float64	1.0
SVGP.kernel.kernels[0].lengthscales	Parameter	Softplus		True	()	float64	1.0
SVGP.kernel.kernels[1].variance	Parameter	Softplus		False	()	float64	0.009999999999999998
SVGP.likelihood.invlink.epsilon	Parameter	Sigmoid	Beta	False	()	float64	0.0010000000000000002
SVGP.inducing_variable.Z	Parameter	Identity		False	(20, 1)	float64	[[0.5488135...
SVGP.q_mu	Parameter	Identity		True	(20, 3)	float64	[[0., 0., 0....
SVGP.q_sqrt	Parameter	Softplus		True	(20, 3)	float64	[[1., 1., 1....

Running inference#

[6]:

opt = gpflow.optimizers.Scipy()

opt_logs = opt.minimize(
    m.training_loss_closure(data),
    m.trainable_variables,
    options=dict(maxiter=reduce_in_tests(1000)),
)
print_summary(m, fmt="notebook")

name	class	transform	prior	trainable	shape	dtype	value
SVGP.kernel.kernels[0].variance	Parameter	Softplus		True	()	float64	136384.63633
SVGP.kernel.kernels[0].lengthscales	Parameter	Softplus		True	()	float64	0.17436090034262242
SVGP.kernel.kernels[1].variance	Parameter	Softplus		False	()	float64	0.009999999999999998
SVGP.likelihood.invlink.epsilon	Parameter	Sigmoid	Beta	False	()	float64	0.0010000000000000002
SVGP.inducing_variable.Z	Parameter	Identity		False	(20, 1)	float64	[[0.5488135...
SVGP.q_mu	Parameter	Identity		True	(20, 3)	float64	[[-0.23227139, 0.6139696, -0.38169821...
SVGP.q_sqrt	Parameter	Softplus		True	(20, 3)	float64	[[0.08247566, 0.07941948, 0.1206941...

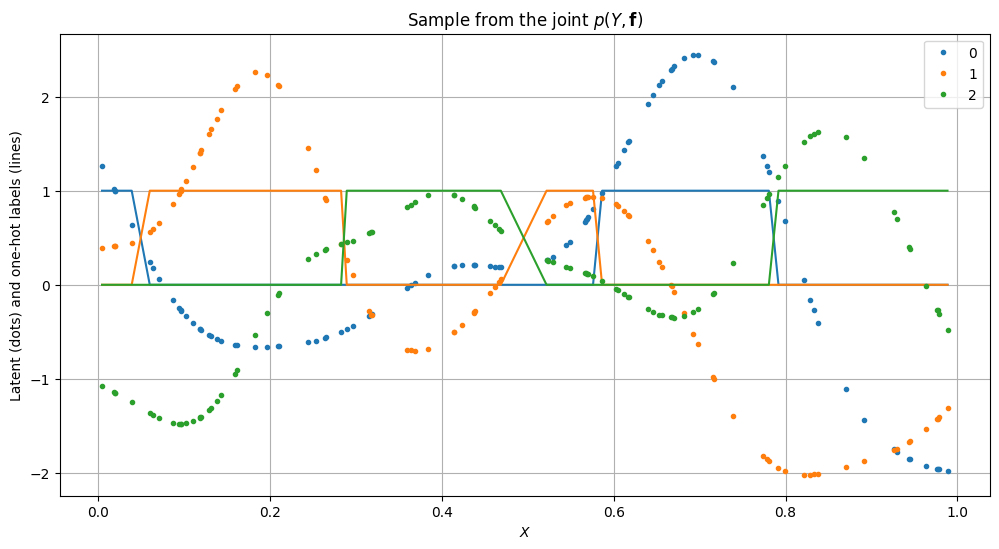
[7]:

plot_posterior_predictions(m, X, Y)

../../_images/notebooks_advanced_multiclass_classification_17_0.png